Double-ended queue¶
Principe¶
Formellement, une "double-ended queue" ou deque est un type de donnée abstrait qui permet insertion et suppression de données à chaque bout (tête et queue).
Plusieurs mises en oeuvres sont possibles parmi celles vues précédemment
- liste doublement chainée
- tableau circulaire
- tableau circulaire dynamique
Ici, on s'intéresse plus particulièrement à l'approche mise en oeuvre par std::deque<T> en C++: un tableau dynamique de tableaux
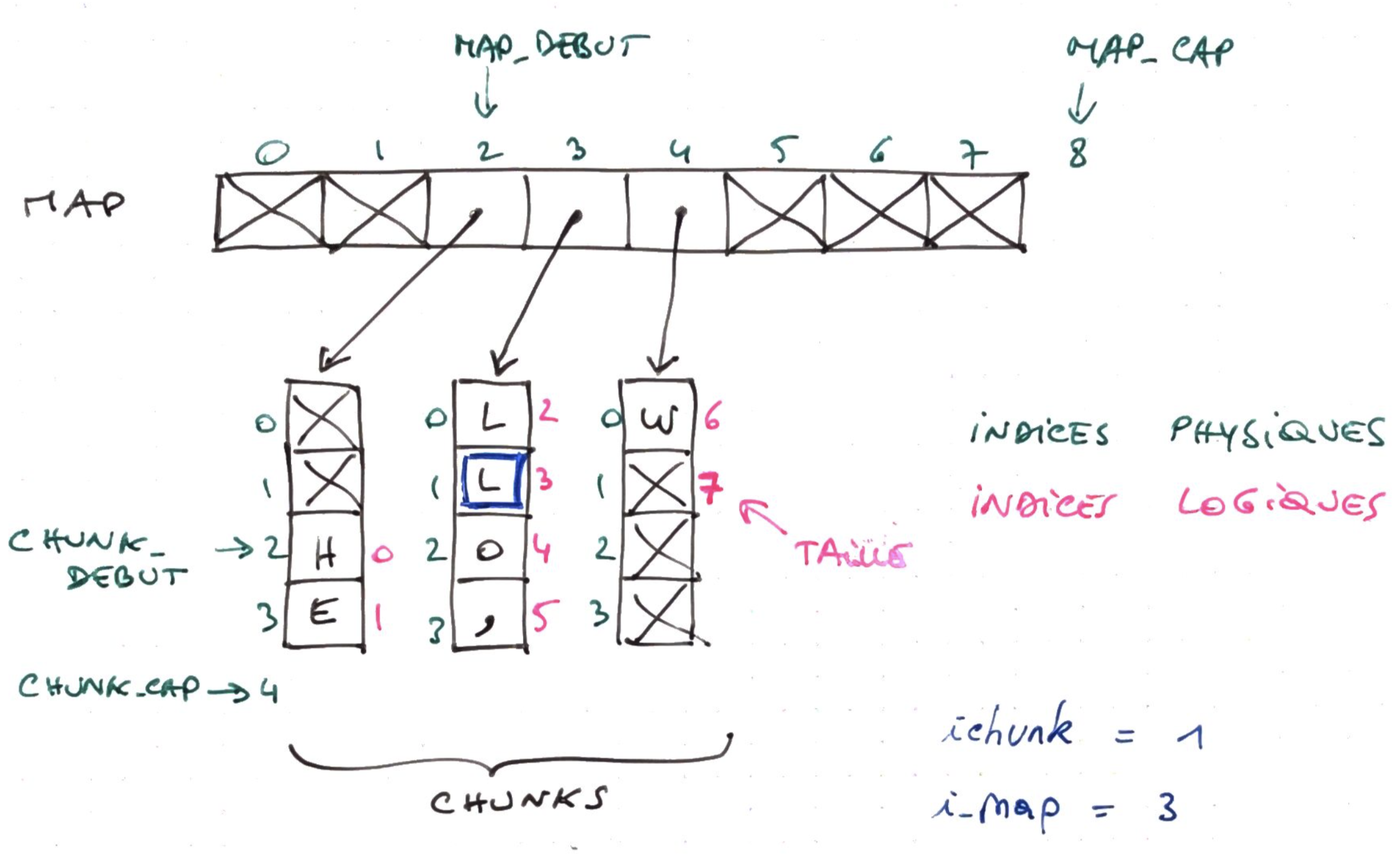
Les données sont stockées dans plusieurs petits tableaux de capacité fixe chunk_cap alloués dynamiquement: les chunks
Les addresses de ces chunks sont elles-même stockées dans un buffer circulaire, la map, de capacité variable map_cap.
Le premier élément est stocké à l'indice chunk_debut du chunk dont l'addresse est stockée dans l'emplacement map_debut de la map.
Les suivants sont stockés aux indices suivants de ce chunk, puis dans les chunks suivants à partir de l'indice 0.
Enfin, le nombre total d'éléments de la deque est stocké dans taille.
Ces 5 attributs et l'addresse du début du tableau map alloué dynamiquement suffisent à localiser tout élément en mémoire.
Ecrivons cette classe DeQue. Le constructeur prend en paramètre la capacité fixe des chunks et la capacité de départ de la map.
class DeQue:
def __init__(self,chunk_cap,map_cap):
self.map = [None]*map_cap
self.map_cap = map_cap if map_cap >= 2 else 2
self.chunk_cap = chunk_cap
self.map_debut = 0
self.taille = 0
self.chunk_debut = 0
Indices physiques¶
Comme dans la mise en oeuvre du buffer circulaire, il est essentiel de pouvoir calculer les indices physiques à partir de l'indice logique i dans [0,n-1] pour n éléments.
Il y en a ici deux
i_chunk, la position deidans son chunk.i_map, le position du chunk deidans la map
On calcule ce dernier en passant par le résultat intermédiaire i_logique_map, l'indice logique du chunk dans le buffer circulaire map.
def indices_physiques(deq,i):
i_chunk = ( i + deq.chunk_debut ) % deq.chunk_cap
i_logique_map = ( i + deq.chunk_debut ) // deq.chunk_cap
i_map = ( i_logique_map + deq.map_debut ) % deq.map_cap
return i_chunk, i_map
Insertion en queue¶
Ignorons pour le moment le problème de gestion de la capacité de map
def check_capacite(deq,taille_demandee): pass
pour insérer en queue, il faut
- calculer les indices physiques
- allouer le chunk si nécessaire
- écrire à l'emplacement
.map[i_map][i_chunk]
def inserer_en_queue(deq,val):
check_capacite(deq,deq.taille+1)
i_chunk, i_map = indices_physiques(deq,deq.taille)
if deq.map[i_map] == None:
deq.map[i_map] = [None] * deq.chunk_cap
deq.map[i_map][i_chunk] = val
deq.taille += 1
DeQue.append = inserer_en_queue
Pour observer comment la DeQue se remplit, écrivons une fonction affichant son contenu physique.
def afficher_deque(deq):
str = "cc:{} mc:{} cd:{} md:{} t:{} \n".format(
deq.chunk_cap, deq.map_cap,
deq.chunk_debut, deq.map_debut,
deq.taille)
for i in range(deq.map_cap):
if deq.map[i] == None:
str += "None\n"
else:
str += deq.map[i].__str__() + "\n"
return str
DeQue.__str__ = afficher_deque
D = DeQue(8,6)
for i in range(12):
inserer_en_queue(D,i*2)
print(D)
Insertion en tête¶
L'insertion en tête fonctionne de manière similaire. La principale différence est qu'il faut mettre à jour map_debut et chunk_debut
def inserer_en_tete(deq,val):
check_capacite(deq,deq.taille+1)
i_chunk, i_map = indices_physiques(deq,-1)
if deq.map[i_map] == None:
deq.map[i_map] = [None] * deq.chunk_cap
deq.map[i_map][i_chunk] = val
deq.map_debut = i_map
deq.chunk_debut = i_chunk
deq.taille += 1
DeQue.appendleft = inserer_en_tete
Observons son effet sur le contenu de la deque
for i in range(1,15):
D.appendleft(-i)
print(D)
Suppressions¶
Les méthodes de suppression en queue et en tête suivent le même principe.
La suppression en queue est plus simple puisqu'il ne faut modifier que l'attribut taille
def supprimer_en_queue(deq):
if deq.taille < 1: raise IndexError()
i_chunk, i_map = indices_physiques(deq,deq.taille-1)
deq.map[i_map][i_chunk] = None
deq.taille -= 1
DeQue.pop = supprimer_en_queue
Pour la suppression en queue, il faut également modifer les attributs de début de map et de chunk
def supprimer_en_tete(deq):
if deq.taille < 1: raise IndexError()
i_chunk, i_map = indices_physiques(deq,0)
deq.map[i_map][i_chunk] = None
i_chunk, i_map = indices_physiques(deq,1)
deq.map_debut = i_map
deq.chunk_debut = i_chunk
deq.taille -= 1
DeQue.popleft = supprimer_en_tete
Observons leurs effets sur le contenu de la deque
for i in range(14): D.pop()
print(D)
for i in range(4): D.popleft()
print(D)
Accès indexé¶
L'accès indexé est immédiat à partir du calcul des indices physiques
def get_item(deq,i):
if i < 0 or i >= deq.taille: raise IndexError()
i_chunk, i_map = indices_physiques(deq,i)
return deq.map[i_map][i_chunk]
DeQue.__getitem__ = get_item
def set_item(deq,i,val):
if i < 0 or i >= deq.taille: raise IndexError()
i_chunk, i_map = indices_physiques(deq,i)
deq.map[i_map][i_chunk] = val
DeQue.__setitem__ = set_item
for i,v in enumerate(D):
print("D[{}] = {}".format(i,v).ljust(13), end = "")
if i % 4 == 3: print()
Gestion de la capacité¶
Reste à considérer le point laisser en suspens. Que doit faire la fonction check_capacite(deq,taille_demandee) ?
vérifier si la capacité est suffisante.
- début et fin ne doivent pas partage le même chunk
- la capacité réelle est donc
(map_cap - 1) * chunk_cap
calculer la nouvelle capacité à allouer. Typiquement en doublant la capacité actuelle de la map.
augmenter la capacité de la map.
- allouer la nouvelle map
- copier les pointeurs vers les chunks en s'assurant de la continuité des chunks courament alloués
def check_capacite(deq,taille_demandee):
if taille_demandee <= (deq.map_cap-1) * deq.chunk_cap:
return
new_map_cap = deq.map_cap * 2
while (new_map_cap-1)*deq.chunk_cap < taille_demandee:
new_map_cap *= 2
augmente_map_cap(deq,new_map_cap)
def augmente_map_cap(deq,new_map_cap):
new_map = [None] * new_map_cap
new_debut = new_map_cap-deq.map_cap+deq.map_debut
new_map[0:deq.map_debut] = deq.map[0:deq.map_debut]
new_map[new_debut:new_map_cap] = \
deq.map[deq.map_debut:deq.map_cap]
deq.map = new_map
deq.map_cap = new_map_cap
deq.map_debut = new_debut
D = DeQue(8,3)
for i in range(10): D.append(i**2+1)
for i in range(6): D.appendleft(-i**2)
print(D)
D.appendleft(42)
print(D)
Complexités¶
Considérons une DeQue avec une capacité de chunk fixée à $C$, dans laquelle on insère $n$ éléments, avec $n >> C$ pour simplifier. Considérons tout d'abord la complexité spatiale.
La mémoire requise est de l'ordre de de
- $n + C$ éléments pour les chunks
- $n/C$ pointeurs pour la map
Avec $n >> C$, c'est proche de $n$ éléments en tout. C'est donc
- meilleur qu'un tableau à capacité variable qui utilise une capacité jusqu'à $2 n$
- meilleur qu'une liste doublement chainée qui utilise $n$ éléments et $2 n$ pointeurs
Quand la capacité n'est pas modifiée, la complexité temporelle des opérations est constante. Le calcul des indices physiques est plus complexe que pour un tableau, mais n'utilise que
- additions
- division entière
- modulo
en prenant une capacité de chunk exponentielle de 2, divisions et modulo s'effectuent par shift et masquage bit à bit.
b = 8; C = 2**b; n = 12345;
print("b =",b,", 2**b =",C,", n =",n,)
print("n//(2**b) =",n//C,"==",n>>b,"= n>>b")
print("n % C =",n % C,"==",n&(C-1),"= n&(2**b - 1) ")
Modifier la capacité ne requiert que de réallouer et déplacer la map, pas les chunks. La complexité temporelle est donc en $O(n/C)$, ce qui est $C$ fois mieux que pour un tableau simple.
Par contre, l'allocation / initialisation des chunks sera vraisemblablement $O(C)$.
En tout, on a dont une complexité $O( C + n/C )$. Pour $n$ donné, le $C$ optimal est donc de l'ordre de $\sqrt{n}$.
|
© Olivier Cuisenaire, 2018 |